Published
- 38 min read
[読書録]原因と結果の経済学
![img of [読書録]原因と結果の経済学](/_astro/2024-01-25-1.bLfd_Ksy_Z1mv7ce.jpg)
読んだ本
原因と結果の経済学(2017/2/16発売, 225ページ)
感想サマリ
- メタボ健診を受けていれば長生きできるのか
- テレビを見せると子どもの学力は下がるのか
- 偏差値の高い大学に行けば収入は上がるのか
「イエス」と答えた人は多いはずだ。しかし、経済学の有力な研究は、これらをすべて否定している
本書の冒頭はこの文言で始められ、最初から興味が惹きつけられる。本書の文章構成は、
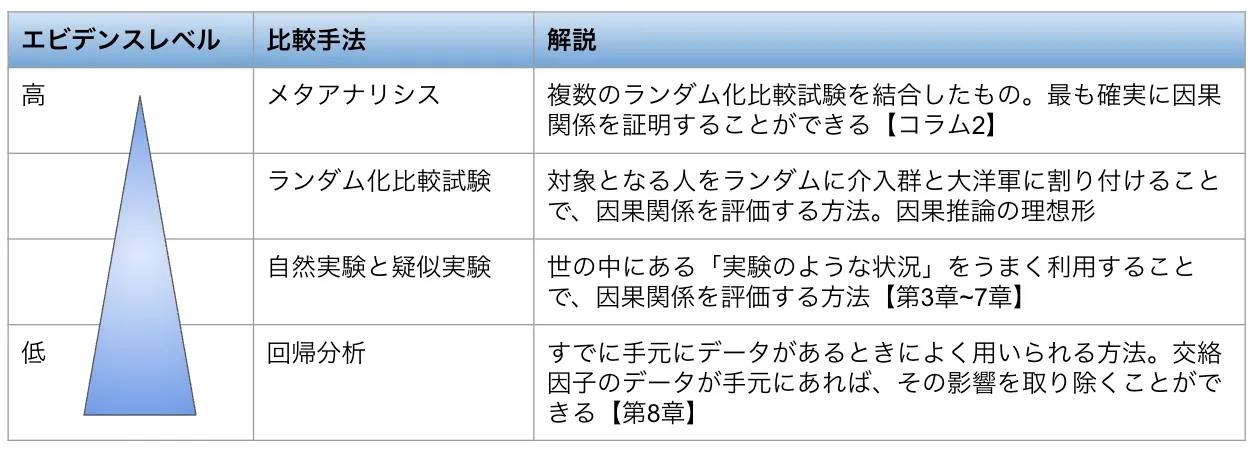 本書p.149 図表1-12から筆者が抜粋
本書p.149 図表1-12から筆者が抜粋
本書内で紹介されているエビデンス・ピラミッドの構造に従って、章が進んでいく。
統計学の知識がない読者であっても、実際に行われた研究結果はどれも実生活に紐づいている内容が多く、ステップを踏みながら、因果関係を見出していく過程が楽しめると思われる。
また、「交絡因子」とか「統計的に有意」とかの統計用語に対する説明もすごく丁寧に書かれているので、読者がそれぞれのステップで脱落しないように配慮されていて、著者の方がすごく丁寧に説明してくれている印象を受けた。
ビジネス用語でも「アップルトゥアップル(Apple To Apple)」という用語が使われることも多いし、各種データを取り扱う際に本当に因果関係があるのか?単なる相関関係なのではないのか?といった疑問を持ちながら、実生活に活かせそうな知識が得られる本だったと感じた。
本書の関連リンク
- 【3分本要約】「原因と結果」の経済学―――データから真実を見抜く思考法 中室牧子 , 津川友介
- 書籍「原因と結果」の経済学 データから真実を見抜く思考法 読書メモ(Zenn)
- 『「原因と結果」の経済学』要点まとめ(Qiita)
内容メモ
はじめに
- メタボ健診を受けていれば長生きできるのか
- テレビを見せると子どもの学力は下がるのか
- 偏差値の高い大学に行けば収入は上がるのか
「イエス」と答えた人は多いはずだ。しかし、経済学の有力な研究は、これらをすべて否定している
多くの人がこれらの問いにイエスと答えてしまうのは「因果関係」と「相関関係」を混同しているからである
- 因果関係がある: 2つのことがらのうち、どちらかが原因で、どちらかが結果である
- 相関関係がある: 2つのことがらに関係があるものの、その2つは原因と結果の関係にないもの
因果関係と相関関係を混同してしまうと、頭った判断のもとになってしまう
因果関係なのか相関関係なのかを正しく見分けるための方法論を「因果推論」と呼ぶ
-
著者の紹介
- 中室牧子:教育経済学者
- 津川友介:医師かる医療政策学者
-
19世紀のアメリカの思想家・作家のラルフ・エマーソンの言葉
-
軽薄な人間は運勢を信じ、強者は因果関係を信じる
-
第1章 根拠のない通説にだまされないために 〜「因果推論」の根底にある考えかた
- 2つの変数が因果関係なのか、相関関係なのかを確認するために、3つの方法がある
- 「まったくの偶然」ではないか
-
2つの変数の関係がまったくの偶然にすぎないのではないかということをまず疑ってみることが重要
- 例)
- ニコラス・ケイジの年間映画出演本数とプールの溺死者数
- ミス・アメリカの年齢と暖房器具による死者数
- 商店街における総収入とアメリカでのコンピューターサイエンス博士号取得者数
-
- 「第3の変数」は存在していないか
- 交絡因子(こうらくいんし):原因と結果の両方に影響を与える第3の変数。相関関係にすぎないものを因果関係があるかのように見せてしまう
- 例)
- 子どもの体力にも学力にも両方影響している「親の教育熱心さ」など
- 「逆の因果関係」は存在していないか
- 警察官の多い地域では、犯罪の発生件数が多いが、これは警察官が多いから犯罪が多いのではなく、犯罪が多いから警察官が多いと考える方が理にかなっている
- 例)
- 警察官の数と犯罪の発生件数
- 「まったくの偶然」ではないか
- 3つが存在しないということを証明するには、仮に〇〇をしなかったらどうなっていたかという反事実を比較する必要がある
-
因果関係の存在を証明するには、原因が起こったという「事実」における結果と、原因が起こらなかったという「反事実」における結果を比較しなければならない
-
- 因果効果: 例)広告を出したときの売上1,500万から広告を出さなかったときの売上1,000万を引いた500万円
- 事実は観察できても、反事実は観察することができないのが問題
- 広告ありのグループと広告なしのグループの比較における課題
- 条件として、広告ありのグループと広告なしのグループが「比較可能」であること
-
2つのグループにおいて、人口や平均的な所得、流行の感度など、宝飾品の売上に影響しそうなすべての特徴が似通っていて、2つのグループの唯一の違いは「広告を出したかどうか」だけだとすれば、この2つのグループは「比較可能」であるといえる。
-
素晴らしい偉業を達成した人のサクセスストーリーは、事実の部分だけしかとらえておらず、反事実はわからない
- 2章以降で行っている目標は、「比較可能なグループを作り出し、反事実をもっともらしい値で置き換える」ということ
- エビデンス・ピラミッド
- メタアナリシス:複数のランダム化比較試験を統合したもの。最も確実に因果関係を証明することができる
- ランダム化比較試験:対象となる人をランダムに介入群と対照群に割り付けることで、因果関係を評価する方法。因果推論の理想形
- 自然実験と疑似実験:世の中にある「実験のような状況」をうまく利用することで、因果関係を評価する方法
- 回帰分析:すでに手元にデータがあるときによく用いられる方法。交絡因子のデータが手元にあれば、その影響を取り除くことができる
第2章 メタボ健診を受けていれば長生きできるのか 〜 因果推論の理想形「ランダム化比較試験」
- ネズミを用いた実験では、病気のネズミを「ランダム」に2つに分けて、投薬したネズミ(介入群)と投薬しなかったネズミ(対照群)を比較する
- 介入群に振り分けられる確率がすべてのネズミで同じような振り分けを「ランダムに割り付ける」と表現する
-
ネズミはもともと個体差があまりないし、数をたくさん用意してランダムに割り付けておけば、ネズミの個体差による偶然に左右されることもない
- ランダム化比較実験では、「介入群がもし投薬をしなかったら」という反事実を、対照群で穴埋めしようとしている
-
「介入」とは、原因と結果の「原因」となるもの(ここでは健診)を、研究対象となる人に与えることを意味する
- 経済学用語のセレクション・バイアス
- 人間が行う「選択(セレクション)」の結果、研究の対象となる2つのグループが比較可能ではなくなってしまうこと
- 英語の日常会話では「リンゴとオレンジの比較」で例えられる
- 統計的に有意
-
「観察された差が偶然の産物である確率」が5%以下であるときに、「統計的に有意である」と言い、2つのグループの差は誤差や偶然では説明できない「意味のある差」だということになる
- 5%の考え方は、コイントスの例で考える。4回から5回連続で表が出たら、人間は偶然を疑うようになることが例として挙げられている
- 1回コイントスして、表が1回出る確率は50%
- 2回コイントスして、表が2回出る確率は25%
- 3回コイントスして、表が3回出る確率は12.5%
- 4回コイントスして、表が4回出る確率は6.25%(このあたりから、人間は偶然ではなく、イカサマを考え始める)
- 5回コイントスして、表が5回出る確率は3.125%(このあたりから、人間は偶然ではなく、イカサマだと疑う)
-
- メタボ健診は1,200億円の予算がかかったが、ランダム化比較試験を行っていれば、数%の予算で行うことができた
- 健診(健康診断)と検査(特定の病気の検査を行う)は違う
- 検診には、生存率を上げるエビデンスがある
- 健診(健康診断)と検査(特定の病気の検査を行う)は違う
- ランド医療保険実験
- 1971-1986にアメリカで行われた、3億ドル(約300億円)の研究費を使った大規模な実験
- 対象者をランダムに4つのグループに分け、1つのグループには自己負担割合が0%になるようなグループに入り、他のグループは25%,50%,90%となるように割り付けた
- この実験の結果として、医療費の自己負担割合が高くなると、人々は病院を受診したり入院したりする回数を減らし、国全体で支払う医療費は減少する
- 医療費の自己負担割合の増加は、軽症にもかかわらず頻繁に病院に通う「コンビニ受診」を防ぎ、国全体の医療費の抑制につながる
- 複数の研究をまとめるメタアナリシス(コラム)
- メタアナリシス:複数の研究結果を1つにまとめて、全体としてどのような関係があるかを明らかにする研修手法のこと
- 2016年8月に国立がん研究センターが、「日本人でも受動喫煙によって肺がんのリスクが1.3倍上昇する」ということを示唆した
- JTが反論したが、国立がん研究センターはJTの主張をエビデンスをもとに退けた
第3章 男性医師は女性医師より優れているのか 〜 たまたま起きた実験のような状況を利用する「自然実験」
- 自然実験:誰にも予想できなかった変化によって、あたかもランダム化比較実験を行ったかのような状況を見出すことで、2つの変数の因果関係を明らかにしようとする方法
- 例)法律や制度の変更、自然災害、紛争など
- 外生的なショック:事前に予想できなかった何か
- 本書におけるセレクション・バイアスの解決例:ホスピタリスト
- ホスピタリストは、シフト勤務中にたまたま運び込まれた患者を担当するため、自分の患者を選ぶことができない
- 著者の津川氏の研究によると、男性医師よりも女性医師が担当した患者のほうが0.4%も30日死亡率が低いことが明らかになった
- 日本では低出生時体重児(出生体重が2,500g未満)の占める割合が、他国と比べて高い(日本9.6%、アメリカ8.1%)
- 「小さく産んで大きく育てよ」というのは、帝王切開の負担がある母体を考えると正しそうに思えるが、子どものことを考えると正しいアドバイスではない
- アメリカ、ノルウェー、カナダ、台湾で行われた双子データの研究による - 著者中室氏の研究でも出生時体重が重いほど、中学校卒業時の成績がよかった
- アルゼンチンの受動喫煙対策の自然実験(コラム)
- 公共施設で厳しい帰省を導入したサンタフェ州と換気設備ぐらいの緩い規制で対処したブエノスアイレス市の比較
- 2つの地域では規制が導入された後も喫煙率は変化がなかったが、サンタフェ州では心筋梗塞による入院患者がブエノスアイレスよりも13%も低くなった
- つまり、たばこを吸っていた当人ではなく、受動喫煙を強いられていた人々の健康状態が改善したと考えられる
第4章 認可保育所を増やせば母親は就業するのか 〜 「トレンド」を取り除く「差の差分析」
- 前後比較デザイン:単純に広告を出す前後で結果を比較する分析手法
- 前後比較が使えない2つの理由
- 時間とともに起こる自然な変化(トレンド)の影響を考慮することができない
- 平均への回帰への可能性
- 差の差分析:前後比較デザインを改良したもの。
- 差の差分析を行うには、介入群と対象群のそれぞれにおいて、介入前と介入後の2つのタイミングのデータを入手しなければならない
- 差の差分析が有効であるためには、2つの前提条件が成り立つ必要がある
- 介入群と対照群において、広告を出す前の売上のトレンドが平行である
- 売上に影響を与えるような「別の変化」が起きていない
- 2.の例。あるドラマが放映されたA地区のみ、人気女優がドラマでつけていたネックレスが爆発的に売れた
- ノルウェー、フランス、アメリカなどでは、認可保育所の整備にもかかわらず、母親の就業は増加しなかった
- 東京大学の浅井氏の研究によると、「保育所定員率と母親の就業率のあいだには因果関係を見出すことができない」
- もともと就業意欲の高かった女性は、私的な保育サービス(祖父母やベビーシッター、あるいは認可外保育所など)を利用していた
- 認可保育所の定員の増加は、彼女たちに私的な保育サービスから公的な保育サービスの乗り換えを促しただけで、これまで就業していなかった女性の就業を促したわけではなかった
- 論文の著者の一人である山口氏は、認可保育所の整備が母親の就業に因果関係を持たなかったとしても、子どもの発達や健康にはプラスの影響がある可能性があると指摘している
- アメリカでは、最低賃金の変更は州ごとに行われる
- 1992年前後でニュージャージー州とペンシルバニア州の差を取ることで、最低賃金の上昇が雇用に与える因果効果を推定した結果、最低賃金の上昇は雇用を減少させないことが明らかになった
- スケアード・ストレート:「恐ろしい(スケアード)」と感じさせることで、正しい行動(ストレート)をとることの必要性を学ばせる教育法
- スケアード・ストレートを受講した若者(介入群)のほうが、受講しなかった若者(対照群)よりも、その後の人生で犯罪にかかわる確率が高かった
第5章 テレビを見せると子どもの学力は下がるのか 〜 第3の変数を利用する「操作変数法」
- 操作変数:結果には直接影響を与えないが、原因に影響を与えることで、間接的に結果に影響を与えるような第3の変数のこと
- 本書の例)新聞社の広告料割引キャンペーン
- 操作変数法が成立するための2つの前提条件
- 操作変数は原因に影響するが、結果には直接影響しない
- 操作変数と結果の両方に影響するような「第4の変数」が存在してはならない
- スタンフォード大学のゲンコウ氏の研究
- 「1948年から1952年にテレビを所有していたか」を操作変数とした
- 結果としては、幼少期にテレビを見ていた子どもたちは、小学校に入学した後の学力テストの偏差値が0.02高かった
- 創作活動やスポーツなど、ほかの活動の選択肢が多い経済的に豊かな家庭では、テレビが持つプラスの因果効果は極めて小さくなってしまい、ときにはマイナスになる研究結果もある
- コロンビア大学のカリー氏の研究
- 大学までの距離が近くなれば、通学や下宿費用に影響するため、「17歳時点で住んでいた自宅から大学までの距離」を操作変数とした。
- 研究結果によると、17歳時点で住んでいた自宅の近くに大学が1校増加するごとに、その地域の女性の大学進学率は19%も増加した
- また、大学以上の高学歴を持つ母親の子どもは、早産や低出生体重で生まれる確率が低く、生まれた時の健康状態が良好だった
-
教育はそれを受けた本人だけでなく、次の世代の子どもたちにも恩恵をもたらす。教育は、社会にとって最も割のいい投資の1つと言ってもよいのではないか
- 南カリフォルニア大学のアハーン氏の研究(コラム)
- 2003年のノルウェーで、女性取締役比率が2008年までに40%に満たない企業を解散させるという法律が議会を通過した
- 「法律が施行される前の各企業の女性取締役比率」を操作変数とした
- 研究の結果によると、女性取締役比率の上昇は企業価値を低下させた
- 具体的には、女性取締役を10%増加させた場合、企業価値は12.4%低下したことが明らかになった
- 原因としては、ほかの取締役よりも年齢が若く、取締役の経験がなく、他業種から参入した人が多かった
第6章 勉強ができる友人と付き合うと学力は上がるのか 〜 「ジャンプ」に注目する「回帰不連続デザイン」
- 回帰不連続デザイン:恣意的に決定されたカットオフ値の両サイドで、介入群と対照群が分かれる状況を利用して因果関係を推定する方法のこと
- カットオフ値: 特段の理由もなく決まった恣意的な値(本書では従業員数50人)
- カットオフ値で生じる結果のジャンプ値が、因果効果となる
- 回帰不連続デザインが成立するための前提条件
- 連続変数のカットオフ値の周辺で、結果に影響を与えるようなほかのイベントが起きていないこと
- 例)従業員50人以上の場合、広告を出せるだけでなく、ボーナスも支給されるなど
- 連続変数のカットオフ値の周辺で、結果に影響を与えるようなほかのイベントが起きていないこと
- ピア効果: 友人らから受ける影響のこと
- マサチューセッツ工科大学のアングリスト氏の研究
- 入試の合格ラインぎりぎりで合格したエリート高校生の生徒たち(介入群)とほかの高校に行くことをにいった生徒たち(対照群)を比較した
- 結果としては、ボストンとニューヨークのすべての学校で、カットオフ値の前後でその後の学力の「ジャンプ」は見られなかった
- つまり、勉強のできる友人に囲まれて高校生活を送っても、自分の子どもの学力にはほとんど影響がない
- カナダのサイモンフレーザー大学の重岡氏の研究
- 日本の70歳を超えると医療費の自己負担割合が3割から1割に下がるという制度を利用して、70歳をカットオフ値とした
- この研究は、ランド医療保険実験の中では明らかにですることができなかった高齢者における自己負担割合と健康や死亡率のあいだの因果関係を明らかにした
- 結果としては、高齢者の自己負担割合が低下すると、外来患者数は10.3%増加するが、70歳のカットオフ値の前後で死亡率の「ジャンプ」は観察されなかった
- つまり、医療費の自己負担割合が引き下げられると、高齢者は病院に行く回数が増えるものの、それによって死亡率や健康状態に影響がでることはないということになる
- 1990年代後半のホルモン補充療法研究(コラム)
- 2002年には、ホルモン補充療法を受けた女性のほうが、乳がんの発生率が統計的に有意に高いということがわかった
- その後、ホルモン補充療法を受けた女性のほうが、逆に心筋梗塞のリスクが高いことが明らかになった
第7章 偏差値の高い大学に行けば収入は上がるのか 〜 似た者同士の組み合わせを作る「マッチング法」
- マッチング法:介入群によく似たペアを対照群の中から選び出すことによって、2つのグループを比較可能にする方法のこと
- 本書では、広告を出している30店舗と広告を出していない70店舗の中から、広告を出している30店舗とよく似た店舗を30店舗出してきて比較する例が挙げられている
- 共変量:広告を出すかどうかは店長の裁量によるところが大きいということから、本書では「店長の年齢」が例として挙げられている
- プロペンシティ・スコア:複数の共変量をまとめて1つの得点にしたもの
- プロペンシティ・スコアとは、介入群に割り付けられる確率のこと
- 本書の例。「店長の年齢」「地域の人口」「地域の平均所得」の共変量を用いてプロペンシティ・スコアを計算する
- 共変量のバランスがとれている:マッチングさせた後、共変量の分布が一致していることが確認できること
- プロペンシティ・スコア・マッチングが成立するための前提条件
- 結果に影響を与えるようなすべての共変量が数値化されたデータとして存在していること
- すべての共変量が、プロペンシティ・スコアの計算に用いられているということ
- プリストン大学のクルーガー氏の研究
- 偏差値の高いA大学に進学した学生(介入群)と地元の大学であるB大学に進学した学生(対照群)を比較した
- 結果としては、卒業後の賃金に統計的に有意な差はなかった。ただ、この結論は、マイノリティであるアフリカ系アメリカ人や、両親が大卒ではない貧困家庭の人々にはあてはまらなかった
- カールトン・カレッジの元学長スティーブン・ルイス氏の言葉
-
「問題は、どこが最高の大学か、ということではない。問題は、誰にとって最高の大学か、なのだ」
-
- A/Bテスト:ビジネス版のランダム化比較実験(コラム)
- ダイレクトメールのA/Bテスト結果。簡素で情報の少ないダイレクトメールほど、顧客を増やす効果があった
第8章 ありもののデータを分析しやすい「回帰分析」
- 実際のデータは、単に経済活動の結果を記録したものにすぎないことがほとんどで、分析の目的に沿って収集されたものではない。このような場合、ランダム化比較実験や疑似実験のような手法を利用できないことも多い
- そのようなときには、回帰分析を用いる
- 回帰分析:4つの点があったとき、この4つのあいだを通る「最適な線」を引くことが回帰分析
- 回帰分析には、「単回帰分析」「重回帰分析」の2種類がある
- 単回帰分析:2つの変数の関係を評価する方法。交絡因子が存在していた場合、その影響を取り除くことができない
- 重回帰分析:交絡因子の影響を取り除いたうえで原因と結果の関係を評価することができる
- 飲酒と肺がんのデータに対して、喫煙という交絡因子を固定することで、重回帰分析を行うことができる
- 固定された喫煙量は、0本でもいいし、1日5本でもかまわない
- 経済学における因果推論の歴史
- 1990年代に、ハーバード大学で「ルービンの因果推論モデル」を経済学に取り入れた
- 2015年に刊行された”Casual Inference for Statistics, Socal, and Biomedical Sciences: An Intoroduction”は、早くも因果推論の代表的な教科書と名高い
- 2000年代には、マサチューセッツ工科大学の貧困アクションラボ(J-PAL)の研究者グループが、さまざまな壁を乗り越えて、大規模な社会実験を実施し始めた
- 政策評価:因果推論に基づいて経済の効果測定を行う研究領域のこと。近年その体系化が急速に進展している
- 1990年代半ばに、イスラエル系アメリカ人のジューディア・パール氏が、DAG(因果ダイアグラム)を用いて、因果関係を明らかにする方法を開発した
- 交絡因子の矢印とは逆で、原因から第3の変数に矢印が引けるときには、第3の変数は中間変数と呼ぶ
- 中間変数を重回帰分析などで無視してしまうと、原因の本来の影響を過小評価してしまうことに注意
補論/おわりに
- 内的妥当性:2つの変数のあいだに因果関係があることの確からしさ
- 外的妥当性:研究の対象とは異なる集団に、その介入を行った場合、同じ結果が再現される程度
- 一般に、日本人は心筋梗塞よりも脳梗塞になりやすく、アメリカ人は脳梗塞よりも心筋梗塞になりやすい
- ランダム化比較試験がアメリカ人を対象にしていた場合、日本人でも同様の研究を実施し、リスク低下の効果が確認されて初めて、「外的妥当性がある」と言える
- ランダム化比較試験の限界
- ランダム化比較試験を実施するにはかなりの費用がかかる
- 「外的妥当性」の問題がある
- 倫理的な問題から実施できないことも多い
- 「ランダム化の失敗」が起こることもある
- ランダム化比較試験で得られた実験よりも、実際に社会全体で拡張して導入したときの効果のほうが小さくなってしまうこともある
- 因果推論の5つのステップ
- 「原因」は何か
- 「結果」は何か
- 3つのチェックポイントを確認
- 反事実を作り出す
- 比較可能になるよう調整
- おわりに
- 2016年1月8日のウォールストリートジャーナルによる、「ビッグデータに潜むバイアス、米規制当局が警告」という記事
-
相関関係があるということは、因果関係があるとことを意味しない - 2014年10月のオバマケアに関するシンポジウム
- マサチューセッツ工科大学のジョナサン・グルーバー氏の言葉
-
個人の経験談の寄せ集めはデータではなく、エビデンスでもありません
-